Le SPC

Introduction

Historique

Avec l'évolution technologique du vingtième siècle, l'entreprise est passée progressivement d'une stratègie de détection des rebuts à une stratègie de la prévention. Le SPC s'inscrit dans cette tendance et correspond au cas de la localisation des contrôles.

SPC s'inscrit dans cette tendance et correspond au cas de la localisation des contrôles. Le créateur du SPC est Walter A. Shewart qui travailla au Bell laboratoire et eu pour élève Edward Deming qui enseigna cette discipline au Japon pendant les années 50. Shewart publia en 1931 les principes de la variabilité d'un procédé en distinguant la variabilité d'un procédé en distinguant la variabilité d'un procédé en distinguant la variabilité aléatoire (naturelle) et la variabilté accidentelle. Par la suite la normalisation s'est considérablement développée sous la forme d'environ 60 normes Afnor. Mais ces techniques n'étaient faites que pour contrôler le produit final. Or, la variation d'une caractéristique produit est une somme de variations du process plus une variable aléatoire non maîtrisable.

Pour remédier à ce manquement, la commissionde normalisation "Méthodes statistiques" de l' Afnor crée en 1989 une nouvelle norme réalisée par un gran groupe d'experts provenant d'entreprises grands donneurs d'ordre comme Rhône-Poulenc, Renault Véhicules Industriels, Télémécanique/Schneider, etc... En effet, elle présente la stratégie de mise en place de la MSP pour expliquer l'intérêt de cette méthode et les étapes clefs indispensables à sa mise en place.

Définition du SPC (ou MSP)

Le SPC Statistical Process Control est un élément d'assurance qualité. Son objectif est de maîtriser un processus mesurable par suivi graphique temporel basé sur des fondements statistiques.

Le SPC part de 3 principes de base:

• c'est le processus qui élabore le produit
• le comportement des processus fluctue dans le temps
• les processus ont tendance à se désorganiser et à se dégrader dans le temps

les processus ont tendance à se désorganiser et à se dégrader dans le temps Le SPC est une méthode préventive de gestion de la qualité qui vise à amener tout processus au niveau requis de régularité, de qualité et à l'y maintenir grâce à un système de surveillance permettant de réagir rapidement et efficacement à des dérives, évitant ainsi la production de produits non conformes.

Le SPC concerne donc essentiellement des fabrications de moyennes et grandes séries. Elle trouve naturellement sa place dans le développement de méthodes de gestion et d'assurances de la qualité, standardisées dans les normes ISO de série 9000.

Les buts du SPC

Eviter les coûts dus à la non-qualité

La seule finalité du SPC est de diminuer les variations des caractéristiques clefs du produit final. En effet, le client, qu'il soit interne ou externe à une socièté, exige du fournisseur la garantie que le produit soit livré avec les diverses caractéristiques comprises dans les tolérances fixées par le cahier des charges.

Ne pas satisfaire cette demande peut avoir plusieurs conséquences facheuses au niveau économique pour l'entreprise fournisseuse:

• perdre tout simplement le client au profit d'une entreprise plus performante
• se voir retourner sa marchandise pour non-conformité aux exigences client
• devoir diminuer le prix de vente du produit si ce dernier ne satisfait pas aux exigences du cahier des charges mais dans une fourchette jugée acceptable pour la réception du produit par le client
• diminuer les rebuts internes dans l'entreprise pour non-conformité évidente

Eviter les dérives du processus

Eviter la dérive d'un processus qui tend principalement à aller vers le désordre au sens chaotique du terme et éviter l'irréversabilité de la perturbation d'un processus

Structurer et identifier les responsabilités de chacun sur le processus. En effet, le formalisme introduit par le SPC permet de définir par écrit les responsabilités de chacun. Qui doit prendre la mesure, comment la prendre, les réactions à une dérive, qui contacter en cas de dérive prolongée, etc... Les procédures et instructions rédigées lors de la mise en place d'un suivi statistique aident au suivi du paramètre process

Permettre de réagir à temps sur la variation anormale d'une mesure d'un processus: la mesure, une fois connue, est immédiatement reproduite sur le tracé temporel. Si ce point est jugé hors limite, l'opérateur se doit de réagir. une fois ce problème résolu, le paramètre n'aura été critique que le temps séparant la réaction adéquate à la déviation et l'avant dernière mesure. Il est courant, en gestion de production, de parler du juste à temps; le SPC est en quelque sorte le juste à temps de la réaction.

Avec une carte SPC, il est possible de réagir au plus vite:

• Mettre en application et "mettre vie" aux multiples paramètres clefs mesurables définis par les différentes méthodologies sont assez lourdes à manipuler en temps réel. Elles ont déterminé des paramètres process à suivre, à contrôler. Quelle soit la méthode utilisée (plan d'expérience, analyse statistique, etc...), il faut suivre l'évolution temporelle des paramètre clefs.
• Mettre un outil simple, rapide et puissant de décision, à la disposition de tout le personnele de l'entreprise. Certes, quelques règles de réaction puisent leur fondement dans la théorie des statistiques, mais leurs applications ne relèvent en rien de la connaissance de cette science. Autant les déterminations des relations produits-process peuvent nécessiter l'emploi de statistiques assez complexes, autant les règles de réaction doivent être simples et concises.
• Donner d'une façon systématique et au moment opportun la nécessité de modifier un paramètre du process ou de rechercher la cause de la dévaition. A une personne non habituée à traiter des séries de données statistiques, il n'est pas évident de reconnaître une valeur que nous pouvons qualifier d'étrangère aux autres données. Il y a nécessité de définir la notion de variation d'une dérie de données afin de réagir à une variation qualifiée anormale.
• Permettre grâce à la prise de données quasi instantanée du process, de déterminer les causes de variation qu'il aurait été très difficile de déceler en temps différé.
• Rechercher et archiver la cause des déviations pour éviter, par diverses actions instantannées ou différées à l'événement, qu'elles se reproduisent. On pourra ainsi hierarchiser les paramètres importants ayant une répercussion sur la qualité du produit.
• Donner, par la traçabilité d'un paramètre clefs, une banque de données pour études d'analyses de données.

Mise en place du SPC

La MSP s'accompagne d'une mutation humaine dans les ateliers car elle permet l'auto-contrôle, grâce à un outil d'information et de décision disponible auprès du personnel de production. Cette mutation est indissociable de la mise en place de l'assurance qualité.

Les contrôles statistiques, quelle que soit la fabrication, concernent aussi bien les matières premières que les produits intermédiaires et les produits finis, mais aussi les principaux paramètres de suivi des fabrications, température, pression, densité, pH, etc. Ces paramètres ont en effet une incidence sur la qualité du produit fini en cas de variation sur le procédé.

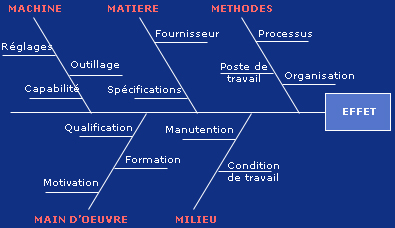
La décision d'implanter la MSP dans une usine ou dans un des secteurs est du ressort du Directeur de l'usine, qui doit jouer le rôle de catalyseur, en créant notamment une Commission de pilotage. Cette Commission, présidée par le Directeur, est composée de tous les chefs de service concernés. Un cadre, en général rattaché hiérarchiquement à la direction, joue le rôle de pilote. Sa mission comporte toutes les prises de décisions concernant l'application de la MSP dans l'usine, et surtout la coordination entre les services impliqués. Il contrôle l'avancement des actions et rend compte au directeur de l'application de la MSP dans l'usine.

La Commission de pilotage doit franchir progressivement les étapes suivantes :

• Effectuer un état des lieux en identifiant les processus prioritaires,
• Choisir le processus où les chances de réussite sont les plus importantes,
• Accumuler les données et effectuer la recherche et la résolution des causes de perturbation du procédé, sans hésiter à effectuer des actions correctives pour diminuer ces perturbations, surtout dans le cas de variations non aléatoires,
• Calculer la capabilité du procédé avec une amélioration du procédé en cas de capabilité inférieure à 1,
• Etablir un plan de surveillance avec la mise en place des cartes de contr ôle appropriées,
• Exploiter régulièrement les cartes de contrôle pour recentrer le procédé en déclenchant des actions correctives.

Les conditions de réussite de mise en place de la MSP doivent être basées avant tout sur une information du personnel tout au long de la mise en place et sur la formation aux statistiques du personnel qui utilise les cartes de contrôle.

La variabilité

L'utilisation de techniques statistiques simples pour conduire un processus de fabrication permet :

• de prévenir les effets de déréglages au lieu de les subir et de trier la production
• d'éviter le contrôle à 100% (contrôle de toutes les unités produites)
• de rationaliser les plans d'échantillonnage (nombre et fréquence des contr ôles) plutôt que de les choisir "par expérience"

Ces techniques statistiques utilisent la méthode d'évaluation de la qualité par le contrôle d'un échantillon limité à quelques unités pour estimer la qualité moyenne de toutes les unités produites.

La variabilité totale d'un processus (statistiquement, la variance v(x)=σ²,carré de l'écart type de la distribution) et la somme des variabilités (variance vi(x)=σi²) de i éléments (matière première, machine, prélèvements, préparation et analyse des prélèvements …) qui le composent : vt(x)=Σvi(x) .

Capabilité du processus de fabrication

La mise sous contrôle de procédés permet de garantir au client, interne ou externe, la recherche dans l'amélioration du procédé, donc du produit.

Cependant le client voudrait pouvoir chiffrer l'amélioration apportée sur le produit reçu. Les indices de capabilité permettent de savoir si on est capable de livrer le produit dans la fourchette demandée et de prouver, par l'emploi d'une politique de qualité, l'amélioration des caractéristiques du produit livré. Les capabilités constituent donc un excellent outil de dialogue entre les partenaires et l'entreprise (et hors entreprise).

Afin de calculer les indices de capabilité du procédé, il faut que les exigences du fournisseur soient clairement définies, que la distribution de probabilité soit normale et que l'échantillonnage soit correct.

En termes statistiques, les indicateurs de capabilité sont définis par :

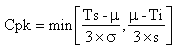
avec Ts : tolérance supérieure, Ti : tolérance inférieure, µ : moyenne, σ: écart-type

Elle représente donc le visé client par rapport au réalisé fournisseur.

Lorsqu'on effectue un contrôle par attributs, la définition de Cpk devient :

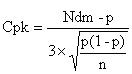
avec Ndm : Nombre de défauts maximal autorisé en % par le client
p : proportion de défauts
n : nombre d'échantillons

Suivant les valeurs de Cp ou Cpk, on classe généralement la capabilité comme :

Le procédé est dit capable si le Cpk est supérieur à 1 : on accepte que 3 pièces sur 1000 soient hors tolérance.

Si le procédé n'est pas capable, alors il est nécessaire d'entreprendre une amélioration du procédé. Comme la loi normale est formée par sommation de causes communes de variation, il est nécessaire d'agir sur le procédé dans sa généralité.

Le contrôle

Généralité

Le contrôle a pour but de vérifier la conformité d'un produit avec les spécifications stipulées par le contrat. Comme il est difficile de tout contrôler, notamment dans le cas de produits fabriqués en grande série, on doit avoir recours à des méthodes statistiques, qui permettent d'analyser le risque de fabriquer un produit de mauvaise qualité. Le contrôle statistique est un contrôle partiel, compatible avec l'organisation "assurance de la qualité" car il donne une bonne image du résultat vrai pour un moindre coût.

Les méthodes statistiques jouent le rôle d'interface entre les données collectées et les résultats, qui serviront à la prise de décision pour prendre des mesures correctives. Le traitement statistique permet de classer, quantifier, sélectionner un ensemble de données pour s'approcher le mieux possible de la valeur vraie en la qualifiant par des notions de fidélité, de justesse, de précision.

Le contrôle peut s'effectuer en cours de fabrication (suivi du produit au cours de son élaboration) ou à un même stade de fabrication (contrôle de réception). Le développement des méthodes de contrôle en cours de fabrication assurant le respect des tolérances a permis de diminuer, voire de supprimer le contrôle final. Il est néanmoins indispensable d'en expliquer la méthode.

Selon que le contrôle porte sur des caractéristiques qualitatives ou quantitatives, on distinguera contrôle par attribut (proportion d'unités non conformes ou nombre moyen de caractères non conformes par unité) et contrôle par variables (proportion de valeurs mesurées non conformes).

Le contrôle de réception

Le contrôle de réception sert à estimer la qualité d'une fabrication, conduisant éventuellement à modifier soit les conditions de réceptions ultérieures soit la fabrication ou le contrôle en cours de fabrication. Se contrôle donc différents aspects de la relation fournisseur-client. Il est très utile de considérer la courbe d'efficacité du contrôle qui exprime graphiquement la probabilité P d'accepter un lot contenant une proportion p d'unités non conformes (hors tolérances).

Dans la norme AFNOR X 06-026 , on a α = 5 % et β = 10 %

Deux points de cette courbe ont une grande importance pratique :

• le risque α du fournisseur :
  Probabilité de se voir refuser un lot contenant une proportion p1 d'unités non conformes que le client pourrait accepter ; cette proportion (ou proportion plus faible) étant acceptée comme ne devant pas normalement conduire au rejet (ici la probabilité d'acceptation est de 1-α)
• le risque β du client :
  Probabilité d'accepter un lot contenant une proportion p2 d'unités non conformes que le client trouvera inacceptable.

Ces 2 risques et les proportions de défectueux définissent en fait 2 points de la courbe par lesquels ne peut passer qu'une seule courbe d'efficacité correspondant à un effectif d'échantillon associé à une proportion de défectueux égale au critère d'acceptation.

Théoriquement on peut définir un prélèvement de contrôle à l'aide de ces 2 points qui permettent de déterminer l'effectif n et le critère d'acceptation A. En fait il est difficile de trouver un plan satisfaisant à ces exigences ne serait-ce que parce que A et n ne peuvent être que des nombres entiers.

En pratique on peut déterminer un niveau de qualité acceptable correspondant à p1 associé à un risque α donné. On peut ensuite fixer la taille n des échantillons. On en déduit un critère d'acceptation A, et à un risque du client donné β correspond une proportion p2 que l'on peut déterminer.

On peut choisir entre différents modes de prélèvements :

• le prélèvement simple : On prend un seul échantillon d'effectif n
• le prélèvement double : On effectue 2 prélèvements successifs ; le contrôle du premier conduit aux décisions d'accepter le lot ou de le refuser ou de prélever le second échantillon ; dans ce dernier cas, les résultats combinés des deux contrôles conduisent à accepter ou à refuser le lot.

Echantillonnage double :

• le prélèvement multiple :
  Ce mode est une généralisation du prélèvement double. La norme NF X022 prévoit 7 prélèvements successifs. Comme dans le prélèvement double, la décision peut intervenir avant le dernier prélèvement.
• le prélèvement progressif :
  On peut considérer que c'est un prélèvement multiple pour lequel le nombre de prélèvements n'est pas déterminé a priori. Les règles d'acceptation, de refus ou de continuation du contrôle s'appliquent successivement à chaque unité contrôlée.

Les cartes de contrôle

Les méthodes statistiques de contrôle utilisées pour maîtriser un processus font appel à la théorie de l'échantillonnage et permettent de définir quand un processus a probablement dérivé en s'aidant des cartes de contrôle.

Dans sa forme élémentaire, une carte de contrôle est un enregistrement chronologique des données caractéristiques d'un processus sous forme d'un graphique, où l'on reporte les moyennes de valeurs d'échantillon par rapport à des limites de contrôle.

Pour un caractère mesuré, on construira une carte de contrôle de la cible centrale et une estimation de la dispersion figurée par l'écart-type s des échantillons ou par leur étendue w (différence entre les valeurs extrêmes de l'échantillon). Ces cartes de contrôle par variables ne feront pas l'objet d'une étude approfondie ; elles seront développées en annexe.

Pour un caractère qualitatif (pièces bonnes ou mauvaises), on estimera à l'aide de cartes de contrôle la proportion de pièces non conformes produites ou le nombre de non-conformités par pièce s'il peut en exister plusieurs. Les variables ne sont pas continues, mais discrètes (discontinues).

Si une fabrication de N unités contient en réalité une proportion p d'unités non conformes, la probabilité de trouver k unités non conformes dans un échantillon de taille n est donnée par la loi binomiale si n < 0.1 N :

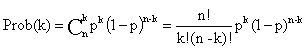
Cette loi peut dans certains cas être remplacée par :

• la loi de Poisson si p < 10% et n > 50
• la loi normale si np > 18

Avant de les utiliser, les cartes aux attributs nécessitent un préambule : la définition d'un critère de conformité. En effet la mesure d'une conformité est souvent le résultat d'un jugement. Or ce dernier peut varier d'une personne à une autre et également pour la même personne en fonction du temps.

Pour réduire cette dispersion de jugement, qui augmente sensiblement la variation de la caractéristique observée, il est nécessaire que la définition de la caractéristique soit très précise.

On met en œuvre cette démarche en 4 étapes :

• Etape 1 : Etablir des normes de référence
• Etape 2 : Mettre au point des aides visuelles appropriées s'il s'agit de défauts
• Etape 3 : Communiquer les normes aux personnes concernées
• Etape 4 : Organiser les systèmes préventifs

Une fois ces précautions prises, on choisit la carte de contrôle. On distingue plusieurs types de cartes :

La carte P

Elle suit la proportion (en pourcentage) d'unités non conformes dans des échantillons de tailles pouvant être différentes.

La taille d'échantillonnages doit être élevée (>50) afin d'être capable de détecter une dérive dans les performances. Il faut que le produit n × p0 > 10 , p0 étant la proportion du nombre de défauts. Il y aura ainsi une convergence vers la loi normale et une bonne sensibilité de la carte.

La carte de contrôle est un diagramme, centré sur p0 et borné par des limites de contrôle Lcs et Lci , sur lequel on reporte les proportions d'unités non conformes trouvées dans les échantillons successifs.

Les limites de contrôle varient en fonction de l'effectif ni :

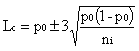
Si p0 est petit et n grand, on fera l'approximation de Poisson et les limites seront :

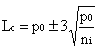
La carte NP

Cette carte est utilisée lorsque la taille n des échantillons est constante. Le principe est le même que pour la carte p, la valeur centrale est n.p0 . Les limites de contrôle sont constantes :

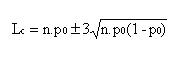
La carte c

Cette carte mesure le nombre de défauts par échantillon. La valeur centrale de la carte est c0 (moyenne des défauts). Si la taille ni des échantillons n'est pas constante, les limites de contrôle sont variables en fonction de chaque échantillon :

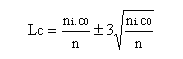
Si l'effectif des échantillons est relativement constant, les limites de contrôle seront :

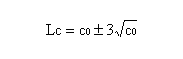
La carte des démérites

L'objectif de ces cartes est de tenir compte non seulement du nombre ou de la proportion de non-conformités, mais aussi de leur gravité. Le principe est de classer par familles les non-conformités trouvées en fonction de leur degré de gravité pour le client.

On détermine ensuite des coefficients de gravité gi tels que Σgi =1 pour chaque famille.

Par définition, le démérite de la production totale estimé à partir de l'analyse des n unités est :

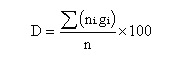
avec ni nombre de non-conformités observées pour chaque famille.

On détermine le démérite de référence

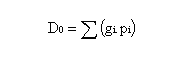
avec pi le pourcentage moyen de non-conformités de chaque famille.

La carte de contrôle des démérites est un diagramme, centré sur D0 et borné par les limites de contrôle, sur lequel on reportera les valeurs successives des démérites. On s'intéresse surtout à la limite de contrôle supérieure Lcs :

Lcs = D0 + 2 à 3 sd avec sd écart type des démérites

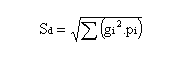
Guide pour l'élaboration, l'utilisation et l'interprétation d'une carte de contrôle

Loi normale

analyse loi normale

Un process de production suit une loi normale si :

• Il est soumis à un grand nombre d’effet (température, jeux, vibration, réglages…)
• Ces différents effets sont indépendants les uns des autres (pas d’interraction forte entre eux)
• Ces différents effets sont d’un ordre de grandeur équivalent.

Dans cette configuration, si l’on réalisé l’histogramme pour l’ensemble de la population, on obtiendrait la courbe suivante.

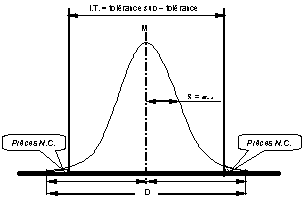
Cette loi permet pour une tolérance donnée de calculer le nombre de pièces non conformes que l’on risque de réaliser.

Avant de réaliser un calcul, il faut s’assurer que la répartition des pièces réalisées par le process suit bien une loi normale.

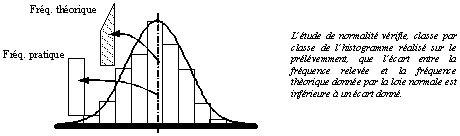
En cas de non normalité, il est nécessaire d’en déterminer l’origine :

• Elle peut être attendue (défaut de forme ou caractéristique unilimites par exemple)
• Dans les autres cas, il faut en déterminer l’origine pour l’annuler et recommencer l’essai

Exemple types de distribution non normales avec les causes probables de non normalité

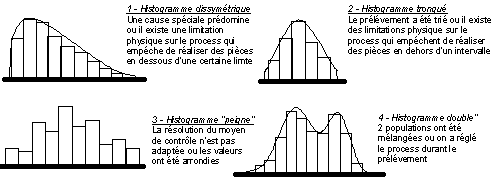
analyse de dispersion

Analysons les 2 cas suivants :

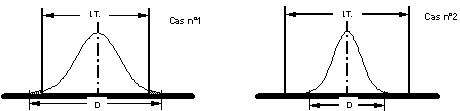
• Cas n°1 : la dispersion est supérieure à la tolérance. On produit donc plus de 0,27 % de pièces en dehors des tolérances. Le process n’est donc pas capable de réaliser la caractéristique demandée sans générer de non conformité.
• Cas n°2 : la dispersion est inférieure à la tolérance. La probabilité de générer des pièces non conformes est très faible. Le process est donc capable de réaliser la caractéristique demandée. Pour être capable, un process doit donc avoir une dispertion inférieure à l’intervalle de tolérance de la caractéristique réalisée.

analyse de centrage

Prenons les 2 cas suivants.

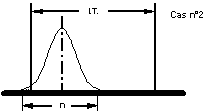
• Cas n°1 : la dispertion est inférieure à la tolérance et la moyenne est situé vers le milieu de l’intervalle de tolérance. La probabilité de réaliser des pièces non conformes est très faible. Le process est donc capable.
• Cas n°2 : la dispertion est inférieure à la tolérance mais la moyenne est décentrée. La probabilté de générer des pièces non conformes devient/li>

Annexes

Définitions

Processus : ensemble d'opérations s'enchaînant dans un certain ordre, permettant l'obtention d'un produit

Capacité : aptitude du système à produire des produits ou des services conformes

Fiabilité : elle mesure la probabilité de fonctionnement sans panne, dans des conditions données et pour une période déterminée

Contrôle : vérification de la conformité d'un produit avec les spécifications stipulées par le contrat

Contrôle par attributs : le jugement d'une caractéristique est fait par tout ou rien. Ce type de contrôle peut être fait à l'œil (aspect, couleur, comparaison à l'étalon…) ou à l'aide de rayons ou d'ultra-sons (analyse de failles, qualité des soudures…)

Contrôle par variables : on mesure quantitativement une caractéristique de façon non destructive(poids, cote, valeur…) ou de façon destructive (dureté, élasticité...)

Carte de contrôle : enregistrement chronologique de données caractéristiques d'un processus, moyenne de valeurs d'échantillons que l'on compare à des limites de contrôle fixées par le cahier des charges du produit

MSP (ou SPC) : outil de prévention permettant de réduire la probabilité d'apparition d'une pièce non conforme

Rebut : produit qui va être rejeté parce qu'il n'est pas conforme aux normes de fabrication

Qualité : aptitude d'un produit à satisfaire les besoins des utilisateurs conformément à leurs attentes et ce au meilleur prix et dans les délais

Ecart-type : l'écart quadratique moyen, ou écart type, est la racine carrée de la moyenne des carrés des écarts des éléments, écarts pris par rapport à la moyenne arithmétique :

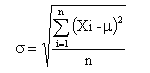
Médiane :La médiane d'une variable statistique est la valeur de cette variable qui partage les individus, supposés rangés par ordre de valeurs croissantes (ou décroissantes), en 2 effectifs égaux