Dossier pour le management de la qualité - n° 67
Comment rendre les statistiques plus appétissantes…
En pesant quelques sachets de M&M's et en comptant leur contenu, vous collecterez des données très utiles. Les tests statistiques sur ces données vous permettront de répondre aux questions sur le poids, la couleur, la qualité et la quantité. Évidemment, si vous vous délectez à l’idée de croquer les confiseries à l’issue des tests, vous serez très motivés par cet exercice…
Résultats obtenus dans le logiciel de statistiques Minitab® 15 en français à partir de la séquence de commandes Stat > Statistique élémentaires > Test t à 1 échantillon. Les résultats du test t incluent une valeur de p de 0,000. La valeur de p étant inférieure à la valeur de α de 0,05, vous rejetez l'hypothèse nulle et concluez que le poids moyen de chaque sachet n'est pas 49,3 g. Vous constatez un poids moyen de 52,040 g, supérieur au poids cible de 49,3 grammes, c’est une bonne nouvelle pour tous les gourmands.
Si deux personnes pèsent à tour de rôle 30 sachets de M&M's à l'aide de la même balance, obtiennent-elles des poids similaires ? Un test t apparié vous aide à répondre. Test T pour données appariées et IC : Poids Personne1; Poids Personne2
Différence des moyennes : limites de confiance (à 95 %) : (-0,02356 ; 0,00956) Test t de la différence des moyennes = 0 (en fonction de la différence 0) : T = -0,86 P = 0,394 Résultats obtenus à partir de la séquence de commandes Stat > Statistiques élémentaires > Test t pour données appariées . La valeur de p de 0,394 est supérieure à la valeur de α de 0,05. L'hypothèse nulle peut être rejetée : il n'existe pas de différence significative entre les mesures moyennes prises par les deux personnes. Test et IC pour une proportion Test de p = 0,15 contre valeur de p supérieure à 0,15
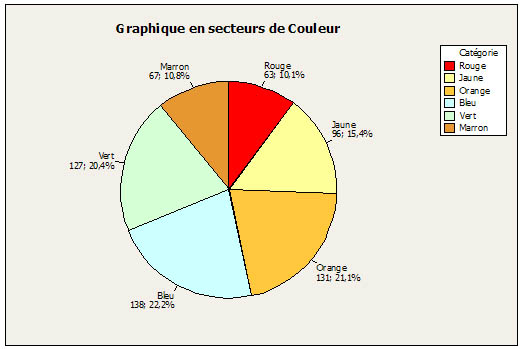
Résultats obtenus à partir de la séquence de commandes Stat > Statistiques élémentaires > 1 proportion. Un graphique en secteurs permet de visualiser le nombre de M&M's de chaque couleur.
L’échantillon contient 138 M&M’s bleus et 63 M&M’s rouges. Cette différence est-elle significative statistiquement ? Utilisez le test d’ajustement du Khi deux pour le savoir. Test d'ajustement du Khi deux pour les dénombrements observés dans la variable : Nombre par couleur Utilisation des noms de catégories dans Couleur
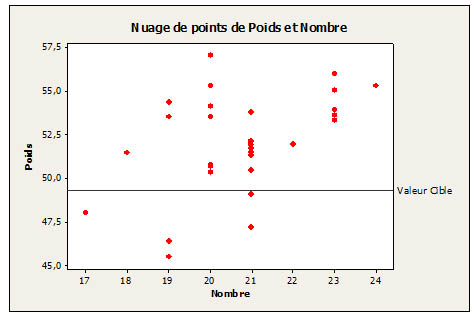
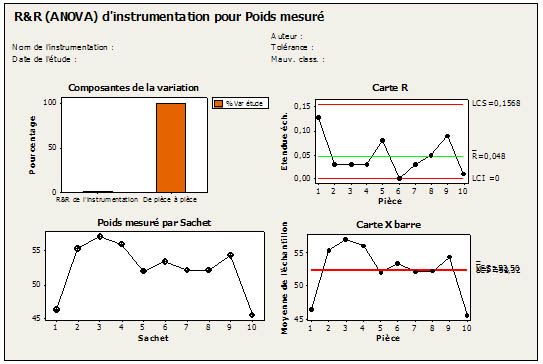
Résultats obtenus à l'aide de la séquence de commandes Stat > Tableaux > Test d’ajustement du khi deux (Une Variable). Corrélation de Pearson de Poids et Nombre = 0,458 Valeur de p = 0,011 Vous pouvez également utiliser les M&M's pour enseigner ou apprendre les techniques statistiques plus avancées telles que l’analyse du système de mesure à l’aide de l’étude de la répétabilité et de la reproductibilité. Avec le logiciel Minitab, créez un plan de collecte de données pour l’étude R&R de l'instrumentation. Ce plan vous guide dans la mesure de 10 sachets de M&M's, chacun à deux reprises, dans un ordre aléatoire. Puis, les résultats obtenus sont analysés dans le logiciel :
Nombre de catégories distinctes = 123 Résultats obtenus à l'aide de la séquence de commandes Stat >Outils de la Qualité > Étude de l’Instrumentation > Étude R&R de l'instrumentation (Croisée). a variation est évaluée à 1,14 %, soit un pourcentage très inférieur à l'idéal de 10 % recherché dans l’étude R&R. Une très faible variation est donc due au système de mesure. Tous les points de la carte R se trouvent dans les limites de contrôle. Ces deux éléments confirment la fiabilité du système de mesure. Nous espérons que vous apprécierez cet exemple (et les M&M's) autant que nous. Cet exercice peut illustrer vos actions de formation ou vos cours, la leçon sera délicieuse ! |